You know when you’re working with kids, and you’re feeling really good about their progress, and about yourself as a teacher, and all of a sudden you ask them something and the answer you get makes you stop dead in your tracks? The answer makes you wonder if you might have misheard, or if you have actually been deluding yourself all year long?
Yeah. So that happened.
To back up: This year in my new role as math coach, one of my jobs is working with small groups of students who need extra support in math. Two of my fifth graders have been enthusiastic participants in math group all year. Fifth grade math, by the way, is hard. These students entered 5th grade on somewhat shaky ground and they’ve been working hard to hold their own, but there’s just so much to hold on to. I admire their tenacity. Both are girls. One is a student for whom English is a new language. They are often quiet in their whole-class math lessons and discussions, but seem to find math group to be a place where they can share their ideas freely, and they often become joyful and animated in our work together.
About a week and a half ago, these two girls (I’ll call them Ariana and Samara) were given some problems around finding volume with fractional units. They were being asked to multiply mixed numbers. The dimensions of the first rectangular prism were 4 ½ x 3 x 2 ½ inches . As they eyed 4 ½ x 3, Ariana said, “So do 4 x 3 and ½ x 3…?”
“Does that make sense to you?” I said, trying to stay neutral. Ariana said that it did, and Samara agreed, but when they went to calculate ½ x 3, they were stumped.
I was a little surprised that ½ x 3 was such a curveball for them. I prompted a little … “So ½ x 3 … you could also think of that as 3 copies of ½ …” and then I waited. (I realize that in some senses, ½ x 3 is not the same as 3 x ½, but I intentionally used commutativity here because I thought it would give them more access.)
“Ohhhh! Yeah! 3 x ½ ! So 3 times 1 is 3, and 3 x 2 is 6, so it’s 3/6,” Ariana said.
Common misconception, right? What’s the big deal? Ariana is certainly not the first kid to begin blindly multiplying stuff because, well, because she can. But. We had done so much work on understanding the meaning of the numerator and the denominator earlier this year! And they did that work in 3rd grade! And in 4th grade! In fact, 3 x ½ is a 4th grade standard problem! What was going on here? I was disturbed.
I put 3/6 and 3/2 up on the board as two possible answers to 3 x ½ . Ariana was certain that it was 3/6, and Samara said she was not sure, but she thought maybe it could be either one.
Wait, WHAT?!
I had them draw a picture to support their ideas. Look at this. (I had to reconstruct the work later because I didn’t realize I was going to write about it until it was over.)
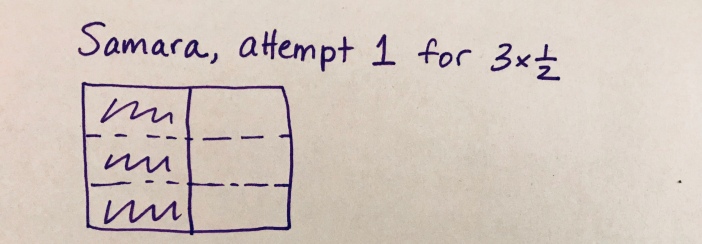
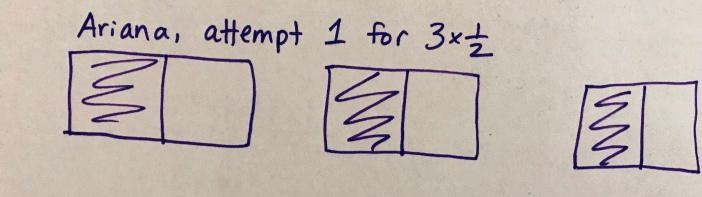
Can you see how both of them used these models to make an argument for 3/6? I was losing my mind, and at the same time, I was kind of loving the challenge. I took a deep breath.
“Samara, your picture shows this,” I said, writing “½ ➗ 3” next to her model. “Can you see why?” She said she sort of could, but sort of couldn’t.
Ariana’s model looked more like 3 copies of ½, but she was still convinced that there were 6 equal parts and 3 of them were shaded, so it must be 3/6. Again, this might all seem normal and understandable except that our curriculum and all of our teaching in 3rd and 4th grade is around developing a deep understanding of unit fractions and the way they work. The language, for example, “3 copies of ½” is intentionally used to help students think about ½ as a unit, and 3/2 as the result of making 3 copies of that unit. How could all of that work have flown out the window?
Our session was over. I sent the girls on their way leaving this question unresolved, but knowing that we’d come back to it next time. After they left, a 4th grader I also work with came into the room and saw the work on the board. I explained what the 5th graders and I had been working on, and that the girls thought 3 x ½ was 3/6. “That’s not right,” my 4th grade friend said.
I felt somewhat heartened. “Why not?” I asked.
“Because the denominator always stays the same,” she said. I deflated again. Was she just repeating a “rule” she’d heard somewhere? Was this an overgeneralization she’d made on her own?
“Why does the denominator stay the same?” I asked.
“Because …” she paused. “Because it’s the unit!”
There are a lot of things to unpack in here. One is the amount of emotional rollercoaster that is involved in teaching for me. Another is the question, how do you know when kids really understand something? And another is the question, can you really understand something as a 4th grader, like the idea that 3 x ½ is 3 copies of ½ or 3/2, and then lose hold of it as a 5th grader when you are trying to hold on to multiplying fractions by fractions, dividing fractions by fractions, dividing whole numbers by fractions, multiplying mixed numbers, 10 to the power of whatever, whole number multiplication and division with numbers of any size, and more? How deep does your understanding have to be for it to be unshakeable, and transferable? What I felt in this conversation was that we were standing on a house of cards.
Today I returned to 3 x ½ with Ariana and Samara. I put up 3/6 and 3/2 again and again asked them to make a representation to support one of these two answers. Both girls started by writing ½ + ½ + ½. This time I asked them to try a number line representation in addition to the other models they had drawn. I asked, “Where does ½ go on this number line?” Here is Samara’s attempt #1 to answer that question:
 I was floored, but I tried to show no emotion as I asked, “How did you decide to put ½ there?” And then she did this:
I was floored, but I tried to show no emotion as I asked, “How did you decide to put ½ there?” And then she did this:
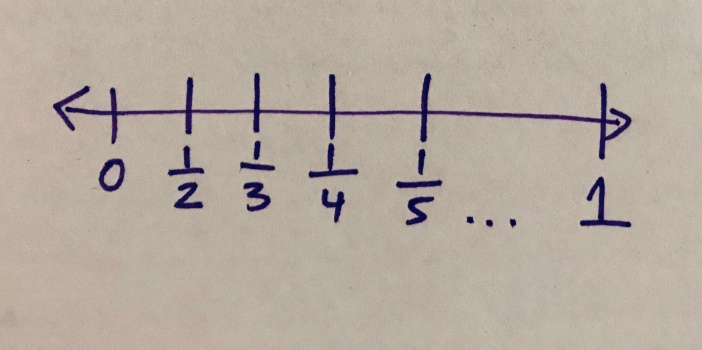
I realized I had to take a further step back. I asked, “What does ½ mean?”
Samara responded, “It’s like you split it in half.”
I took out the pattern blocks. “Can you find a block that represents half of this hexagon?” I asked Samara. She immediately grabbed the red trapezoid. “How did you know?” I asked.
“Because a hexagon has 6 sides and this trapezoid has 3 sides,” she said. (Her class is currently studying attributes of shapes, so it didn’t totally surprise me to hear her say this. It also made me feel like, ahhhh! There’s too much math swimming in this 5th grader’s head!)
Ariana jumped in. “No,” she said. “I don’t agree. Because this hexagon has 6 sides but the trapezoid has 4 sides and 4 isn’t half of 6. I don’t think it’s about the sides.”
“So what makes those halves then?” I asked, with full knowledge that we were now in the territory of 2nd grade standards.
“They’re equal!” Ariana said, and Samara agreed. I put 3 blue rhombuses down on top of the hexagon. “So are these also halves then? They’re equal,” I said.
“No!” Samara said. “Those are thirds.”
“Why?” I asked.
“Because there are three of them,” she said. I put the trapezoids back. “So these are halves because … ?”
Ariana said, “There are two of them and they’re equal.”
So many things had to happen to get to this moment of understanding. First, I had to keep asking questions and trying to draw out the girls’ real, true ideas about fractions. Second, I had to set aside my big feelings about the fact that they didn’t seem to understand things that I really thought they understood, things I had a personal stake in them understanding from all of the work we did together this year. I struggled many times during these exchanges to find the right direction to take the discussion in, to find the right model or counter example that would nudge them toward sense-making. It was so hard. In the course of this discussion, we used equations, area models, number lines, and geometric models to re-engage with content these girls “learned” in 2nd, 3rd, 4th and 5th grades. As their teacher, I had to know all of that content, how it connected, and how it had been taught to them in order to try to pull together a coherent set of experiences for them that would build or re-build their understanding of these ideas.
And after all of that incredibly complex work, where we ended up was: with a maybe understanding of the meaning of one half.
Does your school teach ratios for the first time in 5th grade? Sometimes this causes confusion with fractions. [For some the confusion never quite goes away (see: Simpson’s paradox).]
LikeLike
We follow the CCSS, so we don’t teach ratios in 5th grade, but we do teach the concept of fractions as division, and we also teach the multiplication of a fraction by a fraction, and the division of a whole number by a unit fraction and a unit fraction by a whole number.
LikeLike
Ha, this rings so true Kim. I’m working with a fifth-grader now who is doing incredible work with multi-digit multiplication. It’s going according to plan: for something like 24 x 38, he started with repeated addition. Then he added just a group of ten 24s, and added that sum twice when he needed twenty 24s (2 groups of 10×24) or three times when he needed thirty of them (3 groups of 10×24). He even saw that he would add up 8 more 24s after getting 30 of them. Today he did numbers into the hundreds! He’s taking my little nudges and then making the ideas his own. Pretty soon I’m going to start showing him an area model and maybe even get to the multiplication algorithm before summer. I’m feeling pure awesomeness and everything is a straight line pointing up.
But deep down I gird myself for that bottom to fall out. Like it has thousands of times before. There’s going to be a time when it seems to him like 24 x 38 should be 632 or something like that. It’s coming. An idea that abandons all the earlier sense making.
I love to over-ask “does that make sense?” I give myself mental high-fives when students nod, no matter how meekly. But what does “sense” mean to kids? I bet there are a lot of situations when it reads as “do you think you can remember how to do this again after I say goodbye?” I hope students are integrating new ideas into what they already know. But like you say, there is so much swimming around up there. It’s impossible to tell what’s solid ground.
Lately I’m trying to tell myself that the only thing to do is show students that things connect, with the hope that they start to believe that things connect. Like, we are making a case for sense making, even if “sense making” doesn’t make total sense yet. But sometimes it feels way cooler when they get the answer right.
LikeLiked by 1 person